Concurrency Analysis相关概念

09 June 2023 - 6 mins read time
Tags: program analysis，concurrency

Preface

最近开始阅读Concurrency Analysis相关的paper，主要涉及race condition和deadlock这些领域，记录一下学习中遇到的基本概念。

Causality in Distributed System

对于一个计算系统而言，我们可以把他执行的过程描述成一系列指令或者事件 (Events) 的执行，这个指令或者事件会影响整个系统的状态。例如，我们可以把理想化的CPU抽象成一个有限状态机，每次执行指令都会改变CPU的状态，当然实际的的CPU由于乱序、多发射等优化事实上不是状态机，但是作为一个黑盒来看是没问题的。对于整个分布式系统而言，某个节点中，某个事件的发生可能会影响其他节点的状态，进而影响整个系统，例如：某个节点 a 向节点 b 发送消息，b 收到消息后会将该消息同步给 c 节点，同步消息这个事件显然是发送消息导致的。那么从“时间”概念上讲，发送消息应该发生在同步消息之前。这两个事件之间存在因果关系（cause-and-effect relations）。

那么物理上的时间比如几点几分，几月几日能够描述不同节点之间事件的因果关系吗？

对于分布式系统而言，两个节点可能物理距离很近，例如运行在同一个CPU上的两个线程；也有可能离得很远，甚至不在同一个大陆。两台机器都不在同一个时区，如果使用物理上的时间先不考虑硬件时钟的误差，仅仅是时区之间的转换就比较复杂，效率很低。而且物理上的时间用整数表示会存在冗余，人类公历已经度过了2000多年，表示成整数是一种冗余的信息，因为我们只关注事情的先后次序，不关心事情发生的具体时间，因此需要引入一种特殊的“时间”来记录计算系统中事件发生的时刻。

Happened-before Relation

1978年，图灵奖大佬 Leslie Lamport 发表了一篇名为 Time, Clocks and the Ordering of Events in a Distributed System \(^1\) 的文章，第一次引入了逻辑时钟和happened-before的概念。Happened-before (计作\(\rightarrow\)) 描述了分布式系统中事件发生的因果联系。当且仅当:

1. c 和 e 发生在同一节点并且 c 更早发生 或者
2. c 和 e 发生在不同节点，e 可以通过其他节点发送的消息知道 c 已经发生了

那么事件 c 就可以导致事件 e 的发生，也就是 c happened-before e。

如果两个事件彼此不知道对方是否已经发生，那么可以说两个事件是并发的 (Concurrent)。

下图展示了上文中消息同步的例子的 happened-before 关系，该图描述了分布式系统中的三个节点 a b c，事件节点(a1, b1 …)之间的边描述了事件之间的因果关系。我们可以通过这个有向无环图（Directed Acyclic Graph）来描述事件之间的因果关系。

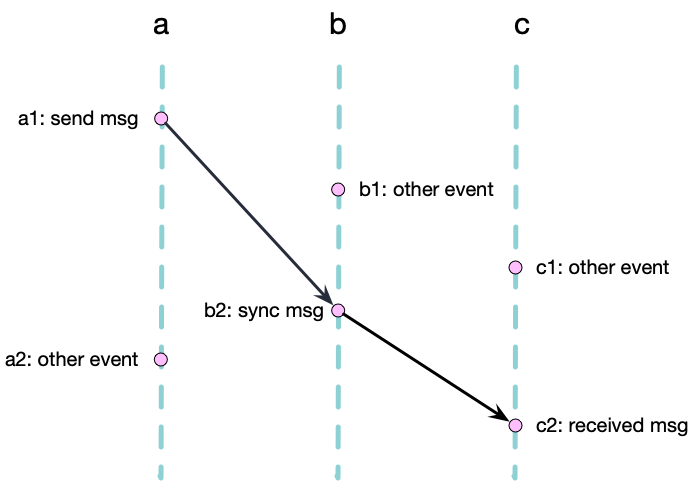
想要知道事件 c 是不是 happened-before 事件 e，我们只需要检查节 c 和 e 之间是不是连通的。例如上图中 \(a1 \rightarrow b2\) 并且 \(b2 \rightarrow c2\)，因此事件 a1 happened-before c2。

Happened-before relation 具有传递性

同理我们可以发现 a1 和 c1 是不连通的 (\(a1 \nrightarrow c1\) and \(c1 \nrightarrow a1\))，即 a1 和 c1 并行，计作 \(a1 \parallel c1\)。

因此我们可以得出结论，两个事件x，y之间可能存在三种关系：

1. 如果 \(x \rightarrow y\)， 则事件 x 可能影响 y
2. 如果 \(y \rightarrow y\)， 则事件 y 可能影响 x
3. 如果x，y之间没有相互影响即 \(x \nrightarrow y\) and \(y \nrightarrow x\)，则x，y是并行发生的 \(x \parallel y\)

从离散数学的角度来看，happened-before关系是一个偏序关系 (Partial Order Relations)，下面简单介绍一下偏序关系。

Partial Order

偏序关系 (Partial Order Relations) 是离散数学中二元关系的一种，主要拥有自反性 (Reflexivity)、反对称性 (Antisymmetry)和传递性 (Transitivity)。

1. Reflexivity: \(a \leq a\) ，every element is related to itself
2. Antiseymmetric: if \(a \leq b\) and \(b \leq a\) then \(a = b\) ，no two distinct elements precede each other
3. Transitivity: if \(a \leq b\) and \(b \leq c\) then \(a \leq c\)

满足这三条性质的二元关系就是非严格的偏序关系，也可以被称作非对称前序关系，如果满足非自反性 (Irreflexivity) 和非对称性 (Asymmetric)，则被称为严格偏序关系：

1. Irreflexivity: not \(a < a\)
2. Asymmetric: if \(a < b\) then not \(b < a\)
3. Transitivity: if \(a < b\) and \(b < c\) then \(a < c\)

通过 Irreflexivity 和 Transitivity 的性质可以推出Asymmetric的性质。

Causal Histories

为了记录事件之间的因果关系，我们可以使用集合来记录事件因果的历史记录。以下图为例，我们给每个事件分配一个唯一的标识符，每个事件的集合取他前驱节点的并集，得到的集合就是该事件的 Causal History。例如事件 b2 的前驱节点有 a1 和 b1，因此 b2 的 Causal History 为 \(H_{b2} = \{a1, b1, b2\}\)。

当一个节点向另外一个节点发送消息时，会将自己的最新的 Casual History 附带在消息中，其他节点收到消息后，会将收到的 Casual History 集合合并到自己本地的 History 集合。例如 b 向 c 发送消息时，会将自己的 History \(H_{b2} = \{a1, b1, b2\}\) 附带在消息中，c 收到消息后，将自己的 History \(H_{c2} = \{c1, c2\}\) 和收到的 History \(H_{b2} = \{a1, b1, b2\}\) 合并，得到 \(H_{c2} = \{\textbf{a1}, \textbf{b1}, \textbf{b2}, c1, c2\}\)。

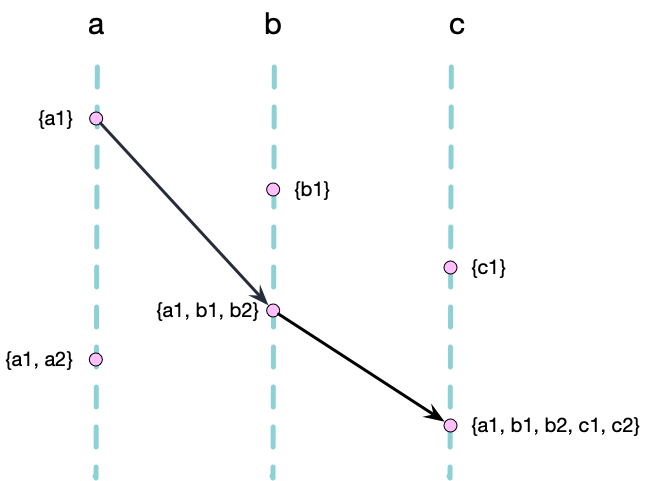
我们可以通过检查事件之间的包涵关系来检查两个事件时候存在Happened-before 关系。当且仅当 \(H_x \subsetneq H_y\) 时，事件 x 可能影响事件 y，即 \(x \rightarrow y\)。这个概念很符合直觉，如果事件 x 影响了事件 y，那么事件 x 的历史记录一定是事件 y 的历史记录的子集。

但是这种集合的表示并不够紧凑，例如上图中的事件 c2，其历史记录为 \(H_{c2} = \{a1, b1, b2, c1, c2\}\)，但是我们可以发现 \(b1 \rightarrow b2\) 并且 \(c1 \rightarrow c2\)，因此 \(H_{c2}\) 中的 \(b1\) 和 \(c1\) 是多余的，考虑到Happened-before的传递性，我们只需要知道每个节点最近发生的事件就足够了，因此我们可以用更加紧凑的方式来表示事件的历史记录。 \(H_{c2} = \{ a\rightarrowtail1, b\rightarrowtail2, c\rightarrowtail2 \}\)

这也就是我们接下来要介绍的Vector Clock。

Vector Clock

Vector Clock 用于确定分布式系统中并发事件的偏序关系，最早可以追溯到1988年的这篇\(^2\)文献。

让我们继续回到上面的例子，\(\{ a\rightarrowtail1, b\rightarrowtail2, c\rightarrowtail2 \}\) 可以被化简为一个简单的向量 [1, 2, 2]，这种紧密的表示已经足以记录每个节点最近的事件。因此我们可以使用这种更加紧凑的向量结构 VectorClock 来取代 Casual History 这种集合的形式。

上文提到我们可以判断两个事件 x、y 的 Casual History 集合是否互为子集来判断是否 \(x \rightarrow y\)。当我们把数据结构换成 VectorClock 后，算法需要做出简单的调整，我们需要检查 \(VC_x\) 是否严格小于 (\(\prec\)) \(VC_y\)，即:

记做:

每当某节点 a 发生一个新的事件，我们不再创建一个新的名字，而是将该节点对应的 VectorClock 中的元素加一，例如 a 发生了新的事件，那么 \(V_a = [1, 0, 0]\) 变成 \(V_a = [2, 0, 0]\)。

最后，Casual History 集合的 Union 操作我们变成取两个向量中对应元素的最大值，只管来讲，我们只需要保留每个节点的最新事件作为时钟，即：

这里仍然以上文中的例子为例，如图所示：

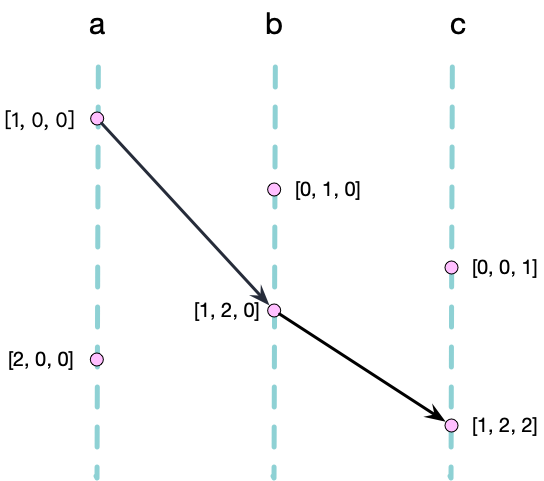
此时我们可以发现，当节点 c 获得来自 b 的消息同步时，其当前的 VectorClock 为[1, 2, 2]，远远比 Casual History 这种集合的表示信息密度更大，可以有效节省存储空间，并且 VectorClock 的 Compare 和 Union 操作都是线性的时间复杂度，效率更高。

Race Condition Detection

了解了 VectorClock 和 Happened-before 的概念，我们可以继续介绍如何使用VectorClock 来检测 Race Condition。Race Condition 在计算机系统中非常之常见，从电路的数据冒险 (Data Hazard)，到上层 web 应用的高并发导致的数据竞争，已经数据库、操作系统中常见的脏读脏写等等，广义上都属于 Race Condition。高并发可以极大的提高计算机系统的吞吐量，同时并发也会导致复杂度的增加，程序员就更容易出错，Race Condition 或许就是性能提升带来的代价吧😂。

现在的大公司的服务端程序基本都是极高的并发量，使用 C++ 或者 Golang 开发，Race Condition 的问题就更加严重，并且 Race Condition 在大型系统中非常非常难以复现，因此在开发或者测试的过程中，大公司都会通过各种手段来检测 Race Condition，例如静态分析、动态分析、模糊测试等等。

有一个比较常见的 Race Condition 检查器是 Google 开发的 ThreadSanitizer(简称TSan)，现在被集成到了 LLVM 的 compiler-rt 中，作为LLVM的运行时库的一部分，之后我们或许会做更加详细的介绍（挖坑🌚。

我们这里把 Race Condition 的范围缩小一点，只关注多线程之间的竞争，当不同线程读和写(Read-Write/Write-Read)、写和写(Write-Write)并行执行时存在 Race Condition，例如下面这段代码：

#include <thread>
int x;

void thread1() {
    // race condition
    x = 1;
}

int main() {
    std::thread t1(thread1);
    std::thread t2(thread1);
    t1.join();
    t2.join();
}

这段代码中，两个线程同时访问了共享变量x，这就是一个典型的 Write-Write Race Condition。如何检查这个bug呢？

首先我们先思考一下正确的代码应该是什么样的，最简单的方式，我们应该在访问共享变量 x 的时候加锁，例如：

#include <thread>
#include <mutex>

int x;
std::mutex mtx;

void thread1() {
    // acquire lock
    std::lock_guard<std::mutex> guard(mtx);
    
    // critical section
    x = 1;

    // lock released automatically
}

上述代码是 C++ 使用锁的方式，或者我们也可以将变量 x 声明为 std::atomic<int> x，这样就可以使用原子操作来保证线程安全。假如使用锁来保护数据的读写，我们可以发现锁就是不同线程之间的同步消息，对于线程 t 而言，锁的获得(Acquire)就是相当于从其他线程收到同步消息，锁的释放(Release)就相当于向其他线程发送同步消息。因此，考虑到上文提到的 VectorClock，我们可以使用 VectorClock 来记录每个线程的同步消息，方法大概如下：

1. 每个线程自己维护一个 VectorClock，用于记录自己的事件和收到的同步消息
2. 每个锁维护一个 VectorClock，用于记录锁的同步消息
3. 线程 t 获得锁的时候执行： \(V_{t} = V_{t} \cup V_{lock}\)
4. 线程 t 释放锁的时候执行： \(V_{t}[t] += 1; V_{lock} = V_{t}\)

这样以来，每个线程之间的同步在运行时就可以被记录下来，很显然锁的释放和获得构成了 Happened-before 关系。同时程序的执行往往存在以下约束：

1. 不可以在其他线程释放锁之前再次获得锁
2. 单个线程中的指令是顺序执行的（把CPU和编译器的优化作为黑盒）

因此，不同的 Acq 和 Rel 操作之间的读写操作也存在 Happened-before 关系，如下图所示：

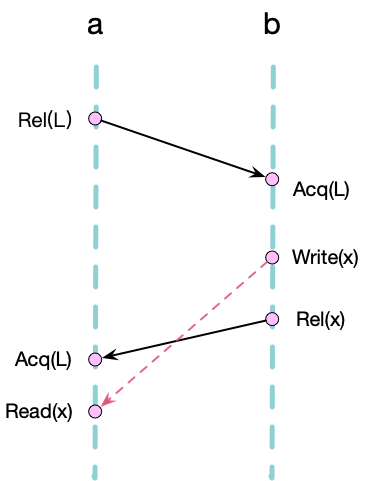
我们可以看到 a、b 两个线程分别读写共享变量 x，并通过锁 L 进行消息的同步，我们可以得到以下关系：

由于Happened-before 关系具有传递性，我们可以得到：

因此 b 线程的写操作和 a 线程的读操作不是并行的，因此不存在 Race Condition。为了记录所有线程对变量 x 的读写操作的时钟，我们可以在全局分别维护两个 VectorClock \(V_R\) 和 \(V_W\)，分别用于记录读操作和写操作的时钟：

1. 当线程 t 执行读操作后，执行 \(V_R = V_R \cup V_t\)
2. 当线程 t 执行写操作后，执行 \(V_W = V_W \cup V_t\)

那么我们如何在运行时检查是否存在 Race Condition呢？我们设计如下算法：

1. 当线程 t 在对变量 x 将要执行写操作时，首先检查 \(V_{Rx} \prec V_t; V_{Wx} \prec V_t\) 即其他线程对 x 读写操作是否 Happened-before 当前线程的写操作，如果不是，则说明存在对变量 x 并行的读写行为，属于 Race Condition。
2. 当线程 t 在对变量 x 将要执行读操作时，首先检查 \(V_{Rw} \prec V_t\)，由于并行的读操作没有副作用，因此我们在读取变量 x 之前，只需要检查是否存在并行的写(Read-Write)操作即可。

码实现如下，这里需要重载 < 和 & 来进行 VectorClock 的比较和合并：

check_write(x):
    if ((V_Rx < V_t) and (V_Wx < Vt))
        V_Wx &= V_t
        return 0;
    else
        throw RaceConditionError;

check_read(x):
    if (V_Rx < V_t)
        V_Rx &= V_t
        return 0;
    else
        throw RaceConditionError;

当然这里还可以继续优化 \(V_R\) 和 \(V_W\) 的数据结构，2009年的一篇PLDI的paper \(^3\) 将 \(V_R\) 和 \(V_W\) 的数据结构优化为了一个叫做 Epoch 的数据结构，把空间复杂度从 \(O(n)\) 降到了 \(O(1)\)。感兴趣的同学可以自行阅读，这里就不再赘述了。

Back to TSan

简单介绍一下TSan，你可以非常方便的使用TSan来检查自己的C++程序是否存在 Race Condition、Dead Lock等情况，他可以在运行时检查存在的线程相关的问题，具体的使用方式如下：

// clang -fsanitize=thread -g -O2 test.cpp
#include <thread>
int x;

void thread1() {
    // race condition
    x = 1;
}

int main() {
    std::thread t1(thread1);
    std::thread t2(thread1);
    t1.join();
    t2.join();
}

用上述命令编译并执行该程序，可以看到如下输出：

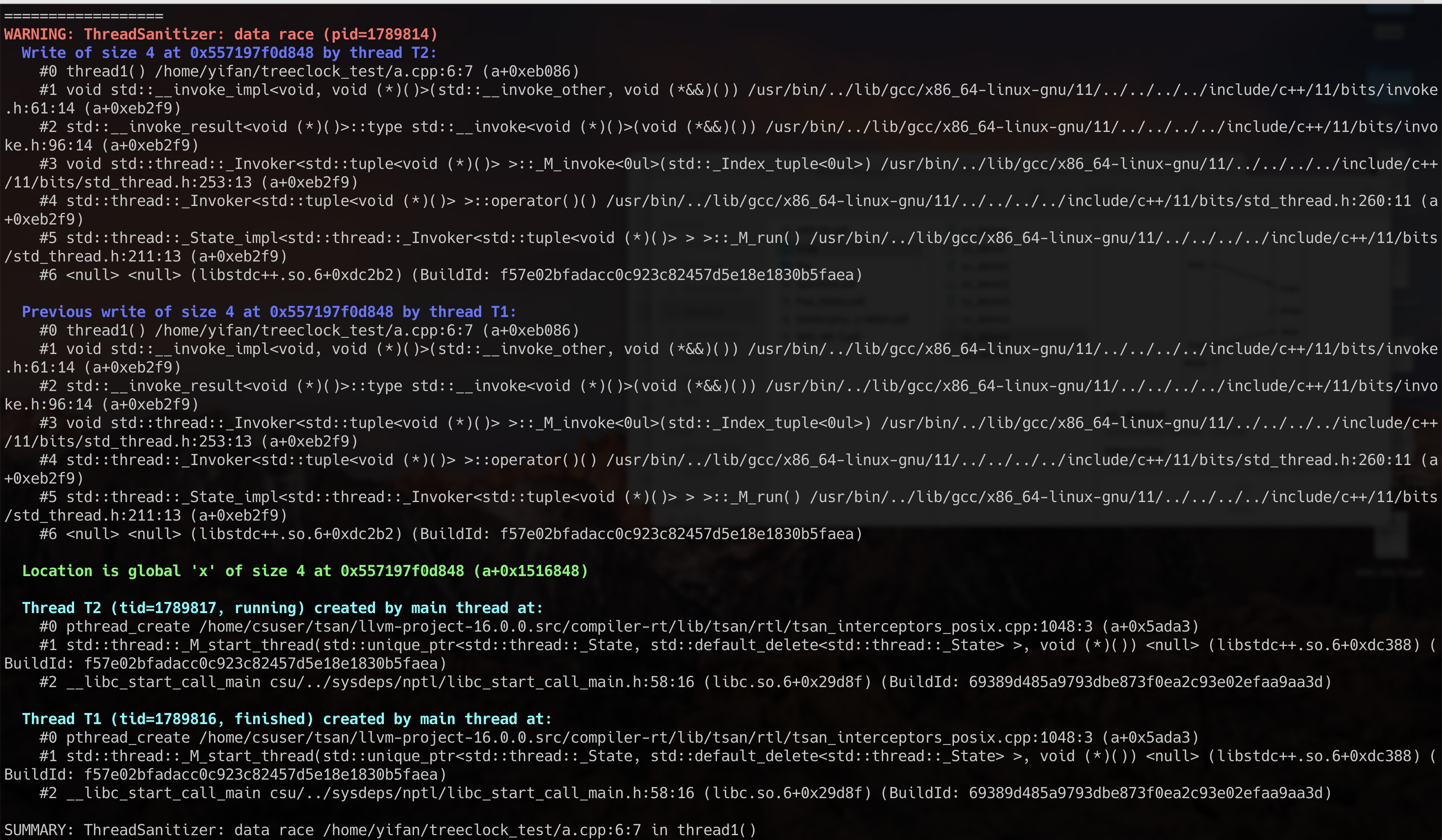
TSan会在编译时对关键函数进行插桩，并在这些关键函数执行的前后更新相关的VectorClock并进行检查，例如:

• pthread_create
• pthread_join
• pthread_mutex_lock
• pthread_mutex_unlock
• …

以 pthread_mutex_unlock 为例：

TSAN_INTERCEPTOR(int, pthread_mutex_unlock, void *m) {
  SCOPED_TSAN_INTERCEPTOR(pthread_mutex_unlock, m);
  MutexUnlock(thr, pc, (uptr)m);
  int res = REAL(pthread_mutex_unlock)(m);
  if (res == errno_EINVAL)
    MutexInvalidAccess(thr, pc, (uptr)m);
  return res;
}

TSan首先会调用 MutexUnlock 函数来更新对应锁的 VectorClock，然后继续执行被 hook 的 pthread_mutex_unlock 函数。

这种检查方式属于静态分析和动态分析的结合，工业界似乎称之为IAST（花里胡哨😂，理论上来说IAST是可以做到没有漏报和误报的，但是由于TSan在实现的过程中考虑到性能问题，把不同的线程非配到了固定数量的 vCPU 上，导致不同线程之间可能抢占同一个 VectorClock，因此会存在小概率漏报(TSan的team自己声称小概率…)，但是仍然不存在误报。

Summary

以上为近期阅读 Concurrency Analysis 相关 paper 的一些总结，发现并发是一个大坑，更多琐碎的细节例如：

1. 不同硬件的 Memory Model（Arm 的 weak model 和 Intel TSO） 的区别
2. 不同编程语言的 Memory Model
3. 编译器的优化例如指令调度
4. CPU的优化（cache的同步、多核的同步、乱序执行、多发射等等）
5. …

以上因素对并发程序的正确性和运行效率都存在深远的影响，同时也存在着很多挑战和机会等着我们去探索。

Reference

1. Time, Clocks and the Ordering of Events in a Distributed System, by Leslie Lamport
2. Virtual Time and Global States of Distributed Systems, by Friedemann Mattern
3. FastTrack: Efficient and Precise Dynamic Race Detection, by Cormac Flanagan, Stephen N. Freund
4. Why Logical Clocks are Easy, by Carlos Baquero, Nuno Preguiça