SSA相关知识(1)--Dominator Frontier

09 July 2020 - 4 mins read time
Tags: compiler

  和好哥们一起参加了毕昇杯编译系统大赛，要手撕一个编译器，邢神带我们搞，按照llvm的结构进行设计，并且把YuLang的部分代码直接迁移了过来，我目前的感受是，这个项目的扩展性真的好。我主要负责平台无关优化，由于存在PassManager这种结构，所以我只需要写相关的pass即可完成优化，不得不说这种设计是真的神奇。

  由于前端直接生成SSA较为复杂，因此yulang的变量分配并不是纯SSA，使用alloc/store的方式来规避phi节点等其他问题，这也是llvm所支持的IR(如下代码)。因为LLVM本身具有一个mem2reg的pass来实现将alloc转为寄存器变量。我接下来也要实现这个pass然后才能进一步优化。

def b():i32 {
    var a : i32[3]
    a[1] = 2
    0
}

对应的IR：

define internal $0f$i32 @_$b_ {
@args:
  %1 = alloca $pi32
  jump %0
@func_exit: ; preds: %0
  %2 = load i32, $pi32 %1
  return i32 %2
%0: ; preds: @args
  %3 = alloca $p$3ai32
  %4 = access elem $p$3ai32 %3, constant i32 1
  store i32 constant i32 2, $pi32 %4
  store i32 constant i32 0, $pi32 %1
  jump @func_exit
}

SSA简介

  SSA（static single assignment form）即静态单赋值，之所以称之为单赋值，是因为每个名字在SSA中仅被赋值一次。他的好处主要体现在：其 Use-Define chain 相当明确，而且每个仅包含单一元素。关于Use-Define可以看这几个知乎回答。举例来说：

 y := 1
 y := 2
 x := y

  从上面的描述所知，第一行赋值行为是不需要的，因为y在第二行被二度赋值，y的数值在第三行被使用，一个程式通常会进行定义可达性分析（reaching definition analysis）来测定它。在SSA下，将会变成下列的形式：

 y1 := 1
 y2 := 2
 x1 := y2

  基于这种形式的IR，我们再做常量传播、dec等优化就会变得更加简单。我这最近一直在读《Engineering a Compiler》这本书，在第9章数据流分析部分才讲了SSA的构造方式，我之前看第5章IR部分的时候没学会，一直以为是智力问题…后来才知道那只是个概念介绍。

0x01 SSA构造算法

经典构造法

本书中介绍的算法是相当经典的算法，感兴趣的可以看论文《Efficiently computing static single assignment form and the control dependence graph》，大概就是：

  1. 遍历 IR 构造 CFG
  2. 计算支配边界
  3. 确定 Phi(Φ) 函数位置
  4. 变量重命名

关于CFG的构造算法，大致如下：

Basic Block构造算法：

  1. 找基本块入口源代码的首行或者转移代码（有条件和无条件）或者转移代码的下一行
  2. 基本块构造：通过入口点开始，将其组成各自的基本块。基本块语句序列的特征：从不包含它本身的进入点到其他进入点或者到某条转移语句或者到某条停止语句
  3. 如果有语句不在任一基本块中，那么它为 ”死代码“，删除

当确定Basic Block后，紧接着构造 CFG:

如果在一个有序代码中，基本块 B2 跟在 B1 后，那么产生一个由 B1 到 B2 的有向边。

  1. 有跳转点。这个点从 B1 的结束点跳到 B2 的开始点
  2. 无跳转点（有序代码中），B2 跟在 B1 后，且 B1 的结束点不是无条件跳转语句

这里推荐去听b站李樾老师的《软件分析》课程，讲的非常好。

接下来是计算支配边界，在生成SSA的时候，需要计算在何处插入正确的 Φ (phi-function)。例如：

if (b > 2) {
    a++;
} else {
    a--;
}
b = a;

此时形成的IR应该是这样的：

  branch %b0, %1, %2
@if_end: ; preds: %1, %2
  b1 = phi(a1, a2)
  store i32 constant i32 0, $pi32 %3
  jump @func_exit
%1: ; preds: %0
  a1 = a0 + 1
  jump @if_end
%2: ; preds: %0
  a2 = a0 - 1
  jump @if_end

cfg大致如下： cfg

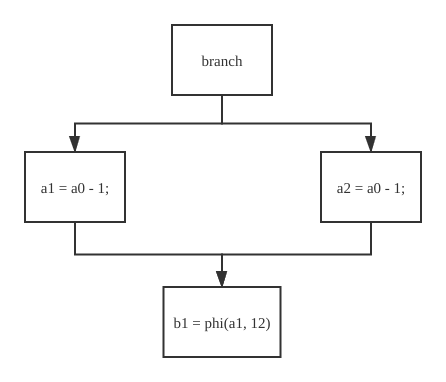
  这里可以发现一个问题，b = a赋值的时候，我们需要确定到底是选择a1还是a2,因此需要插入一个phi函数。计算在何处插入正确的 Φ ，一种方法是在所有有多个前驱的Basic Block的开头插入 Φ-node，但是这种方法会插入很多的无用的 Φ-node ，有很多 Φ-node 的参数都是相同的一个定义。

  这样得到的 SSA 形式的 IR，占用过多的内存，增加了计算的开销。任何使用该SSA进行代码分析或者优化的过程都会浪费很多计算资源。为了减少 Φ-function 的数量，首先想到的方法就是确定插入 Φ-function 的精确位置。

0x02 支配性(Dominance)

  在入口结点为b0的流图中，当且进当bi位于从b0到bj的每条路径上时，结点bi支配bj，写作 bi dom bj。根据定义，bi dom bi。

举个例子：

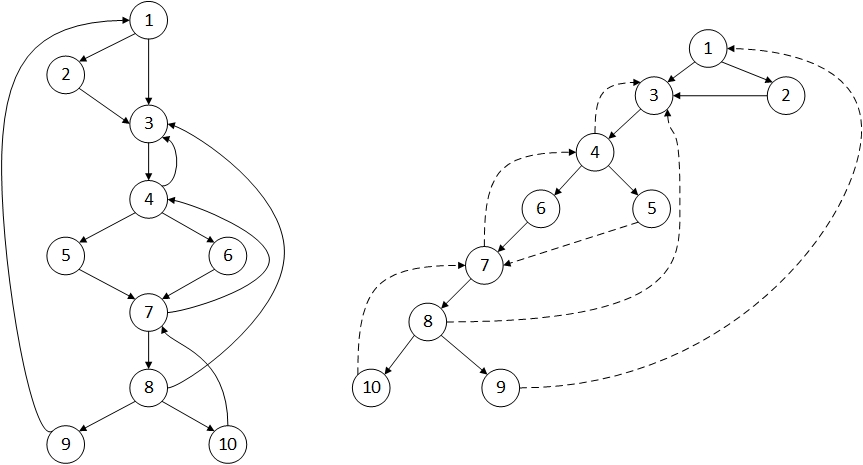
graph

  在这张图中结点1支配所有的节点，因为他是入口结点，所以到达每个结点都必须经过它。结点2只支配他自己，因为没有结点必须经过2。

  另外一个比较重要的概念就是 strictly dominates（严格支配），如果 d != n 且 d dom n， 那么 d sdom m，例如上图中 4 sdom 5。说白了就是不是自己支配自己。n的严格支配集记做 SDom(n)，该集合中，与n最近的结点称为n的直接支配结点 (immediate node)，记做 IDom(n)。cfg的entry没有直接支配结点。例如5的直接支配结点是4,7的直接支配结点也是4.

\[SDom(n) = Dom(n)-\{n\}\]

  那么如何计算支配域Dom(n)呢，参考《Engineering a Compiler》这本书中的不懂点算法，下面给出介绍，非常刺激，核心就一句话，如下：

\[Dom(n) = \{n\}\cup(\mathop{\cap}\limits_{m \in preds(n)} Dom(m))\]

其实上面这个公式的意思就是，求n的前趋的支配域的交集然后并上{n}，具体的迭代算法过程为：

iter

  一直迭代CFG的Dom集合，直到不发生变化，即到达fixed point，至于这个迭代算法为什么能停下来我这里就不证明了，

0x03 支配者树(Dominator Tree)

  这个概念比较好理解，根据cfg的支配信息，建立一个支配树，如下图所示：

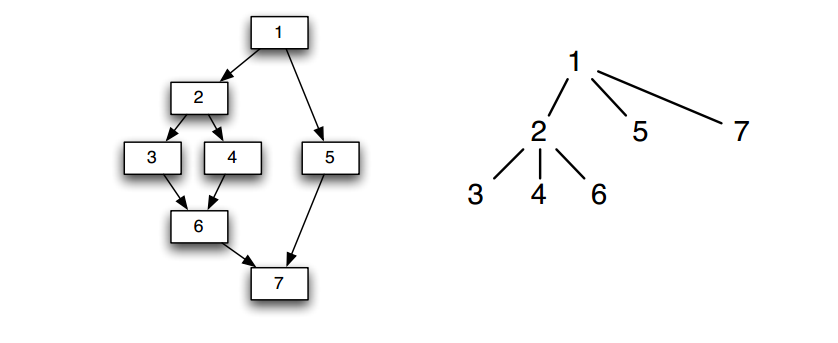
dominator_tree

  该树的边使用一种简单的方式编码了IDom集合。若m为IDom(n),则支配者树中必然有一条边从m指向n，即n为m的子结点。比如3,4,6都是2的子结点，尽管6并不是2的直接后继。

因此根据上面的算法计算出的Dom信息，我们可以很容易的建立Dominator Tree,这里给出树上的数据展示：

  B0 B1 B2 B3 B4 B5 B6 B7 B8
Dom {0} {0,1} {0,1,2} {0,1,3} {0,1,3,4} {0,1,5} {0,1,5,6} {0,1,5,7} {0,1,5,8}
IDom N 0 1 1 3 1 5 5 5

然后根据Dom值计算出IDom值，实际上IDom值就是其父结点，然后根据IDom值构造Dominator Tree即可。

cfg

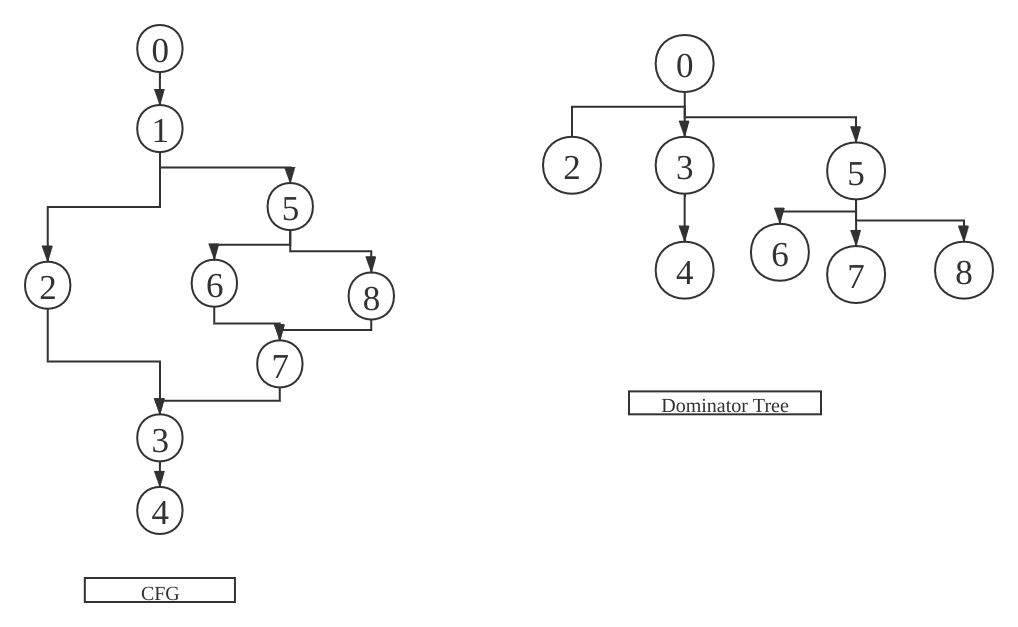
0x04 支配边界(Dominator Frontier)

  在构造SSA的过程中，若考虑使用最大静态单复制会导入大量的phi-function，比如，假如CFG中结点n中的一个定义，该值到达某结点m时，若 n Dom m 则该值并不需要phi-function，因为该定义只用一种情况才能导致无法传播到m，就是在n、m之间重新定义了该值。

因此只有在n的支配域外的汇合点，才需要引入phi-function，这就是支配边界，即：

  1. n支配m的一个前趋
  2. n并不严格支配m

有这种性质的节点m集合称为n的支配边界，记做DF(n)，例如上图中 DF(2) = 7

\[DF(n) = \{m\mid q \in preds(m), n \in Dom(q)\}\]

说人话就是，所有最近不能被n严格支配的节点的集合就是DF(n)，即支配边界。如下图，DF(5) = {4, 5, 12, 13}

df

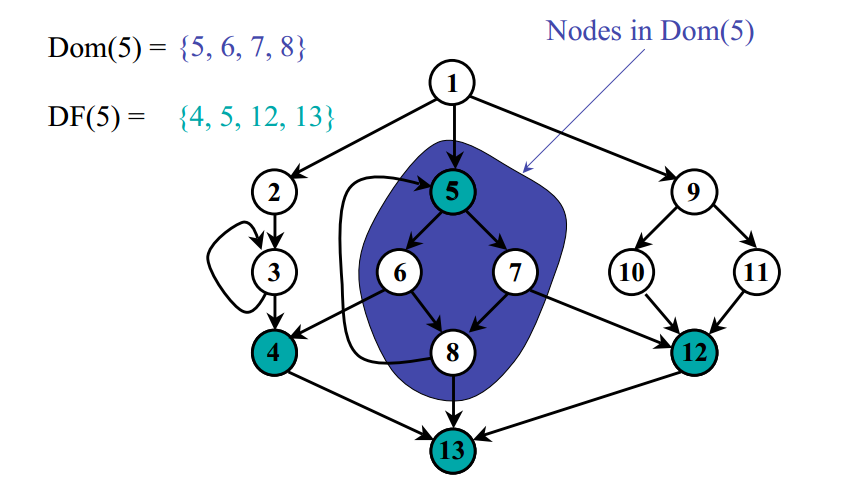
可是支配边界的作用是什么呢？我们上面已经解释过了，只有在到达结点 n 的支配边界的时候，才需要考虑其他路径是否有对 n 结点中某值的定义并且插入适当的 Φ-function。

df1

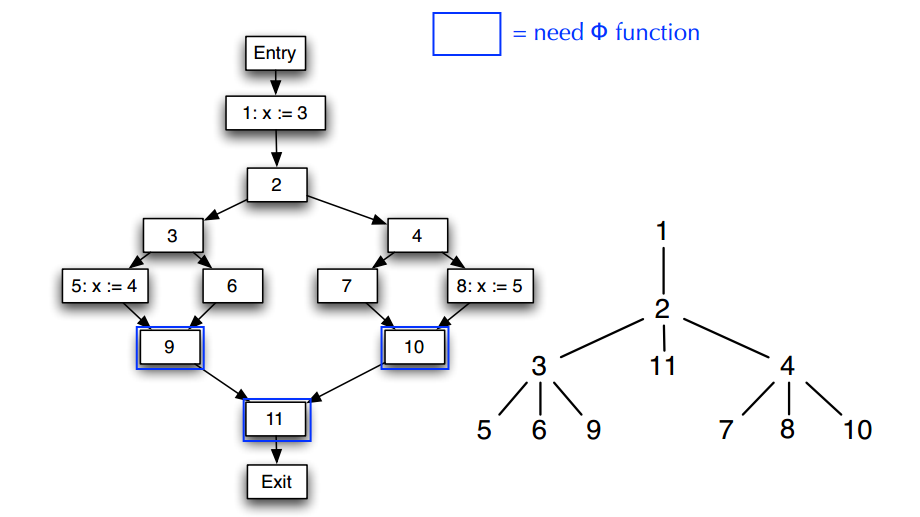
  虽然从结点1的角度来看，它支配结点（例如9，10，11）可能会用到x:3，但并不意味着这些节点里不需要插入ϕ\phiϕ-function的。

  结点 5 定义了值 x := 4，结点 5 没有支配结点并且结点 9 就是结点 5 的支配边界，在这里需要考虑从从其他路径传播到此的对变量 x 的其他定义，也就是结点 1 中的定义 x := 3。所以在结点 9 需要插入一个关于变量 x 的 Φ-function。同理在结点 10 的开头也需要插入一个 Φ-function，另外由于 Φ-function 会产生新的定义，所以也需要在结点 9 的支配边界结点 11 的开头插入 Φ-function。

但是如果要确定支配边界的话，需要先构造出支配者树，然后借助于支配者树来得出支配边界。

0x05 求支配边界

这里直接给出算法伪代码：

for all nodes, n, in the CFG
    DF(n) <- Null

for all nodes, n, in the CFG
    if n has multiple predecessors then
        for each predecessor p of n
            runner <- p
            while runner != IDom(n)
                DF(runner) <- DF(runner) + {n}
                runner <- IDom(runner)

  该算法会定位到CFG中的各个汇合点就。接下来，对j的每个前趋p，从p开始沿着支配者树向上走，直到找到一个直接支配j的结点。按照下图举个例子：

df2

  1. B1 对于其在CFG中的前趋B0，发现B0是IDom(B1)，因此不进入while循环。对于其前趋B3,此时将B1添加到DF(B3)中，接下来进入B1，将B1添加到DF(B1)中，然后前进到B0，然后停止。
  2. B3 对于其在CFG中的前趋B2，发现B2不是IDom(B3)，此时将B3添加到DF(B2)中，接下来前进到B1，而B1是IDom(B3)故停止while循环。对于其前趋结点B7，发现B7不是IDom(B3)，此时将B3添加到DF(B7)中，然后前进到B5，将B3添加到DF(B5)中，然后前进到B1停止。
  3. B7 对于其在CFG中的前趋B6，发现不是IDom(B7)，将B7添加到DF(B6)中，接下来前进到B5，停止while循环。对于其前趋节点B8，将B7添加到DF(B8)，然后前进到B5，然后停止。

于是得到支配边界如下：

  B0 B1 B2 B3 B4 B5 B6 B7 B8
DF Null {B1} {B3} {B1} Null {B3} {B7} {B3} {B7}

0x05 总结

  到这里差不多就结束了，这几个算法比较有趣的点在于，数据流分析的大部分算法都是不动点算法，然而为啥能到达不动点属实是一个需要我们思考的问题，事实上如果一个集合只进行并的运算，那么对其进行迭代往往可以达到fixed point，你想一想是不是;)

阅读量